SOLVED: Q4: a) Define compact, sequentially compact, and countably compact. Discuss the compactness and sequential compactness of the following subspaces of R2. 1) (x, 25/211 < x < 2 2) (x, sin(x-15)/1 <
Topology: Sequentially Compact Spaces and Compact Spaces | Mathematics and Such
Sequentially Compact Space: Topological Space, Sequence, Subsequenc, Limit Point Compact, Compact Space, Limit Point, Bolzano-Weierstrass Theorem, Heine-Borel Theorem, Metric Space, Uniform Continuity - Surhone, Lambert M., Timpledon, Miriam T ...
Real Analysis | Compact set of real numbers. - YouTube
Topology: Sequentially Compact Spaces and Compact Spaces | Mathematics and Such
A metric space is sequentially compact iff it has bolzano weierstrass prperty|UPSC|B.Sc.3rdyr|L38 - YouTube
![SOLVED: Compactness and sequential compactness. Let X = [0,1] × [0,2π] equipped with the product topology. It shows that X is compact, but not sequentially compact. PROVE THAT X is compact, but](https://cdn.numerade.com/ask_images/acafd8d998ac49b384fafd3adff4f32e.jpg "SOLVED: Compactness and sequential compactness. Let X = [0,1] × [0,2π] equipped with the product topology. It shows that X is compact, but not sequentially compact. PROVE THAT X is compact, but")
SOLVED: Compactness and sequential compactness. Let X = [0,1] × [0,2π] equipped with the product topology. It shows that X is compact, but not sequentially compact. PROVE THAT X is compact, but
Topology: Sequentially Compact Spaces and Compact Spaces | Mathematics and Such
DEFINITION -SEQUENTIALLY COMPACT | THEOREM - X IS LIMIT POINT COMPACT THEN X IS SEQUENTIALLY COMPACT - YouTube
![Relations between topological spaces [26]. Hausdorff topological spaces... | Download Scientific Diagram](https://www.researchgate.net/publication/2198506/figure/fig1/AS:394705373286424@1471116502964/Relations-between-topological-spaces-26-Hausdorff-topological-spaces-have-the-property.png "Relations between topological spaces [26]. Hausdorff topological spaces... | Download Scientific Diagram")
Relations between topological spaces [26]. Hausdorff topological spaces... | Download Scientific Diagram
Solved Let K be a sequentially compact set and F = {G_alpha: | Chegg.com
Math | PDF | Compact Space | Metric Space
Definition of Sequentially Compact Metric Space | L13 | Compactness @ranjankhatu - YouTube
Solved 1. Let S ⊂ R be a sequentially compact set. Prove | Chegg.com
I. Sequential Compact and Closed Subsets
Every sequentially compact metric space is totally bounded | Topology | - YouTube
PDF) SEQUENTIALLY COMPACT S^{JS} - METRIC SPACES (Commu. Opt. Theo.)
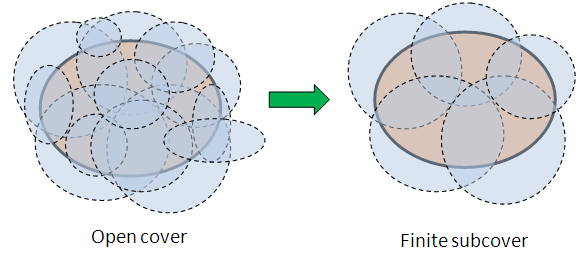
sequences and series - Prove that if $X$ is sequentially compact then given any $\epsilon>0$ there exists a finite covering of $X$ by open $\epsilon$-balls. - Mathematics Stack Exchange
analysis - Sequentially compact $\Rightarrow \inf_{x\in A}\varepsilon_{x}=:2\varepsilon_{0}>0$ - Mathematics Stack Exchange
Topology: Sequentially Compact Spaces and Compact Spaces | Mathematics and Such
sequences and series - Prove that if $X$ is sequentially compact then given any $\epsilon>0$ there exists a finite covering of $X$ by open $\epsilon$-balls. - Mathematics Stack Exchange
Analysis WebNotes: Chapter 06, Class 31
Countably & Sequentially Compact Space | Prove Every Sequentially Compact Space is Countably Compact - YouTube
