Analysis WebNotes: Chapter 06, Class 31
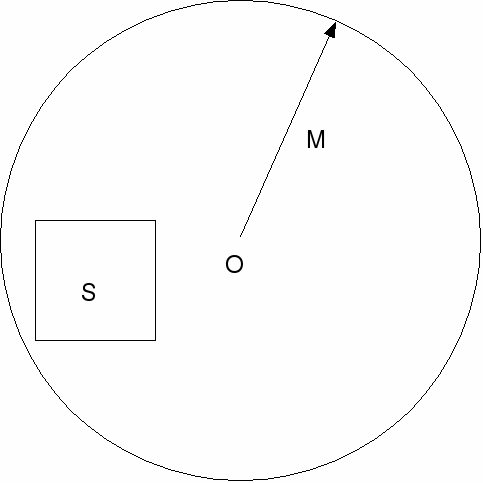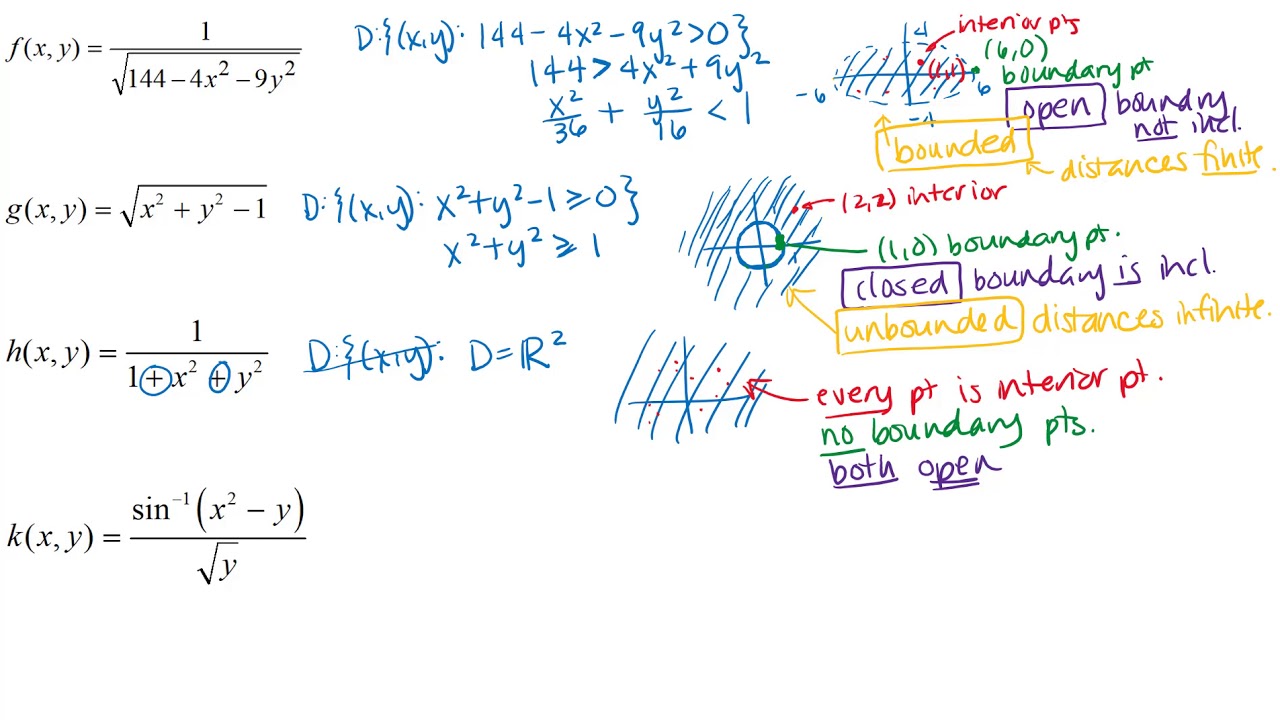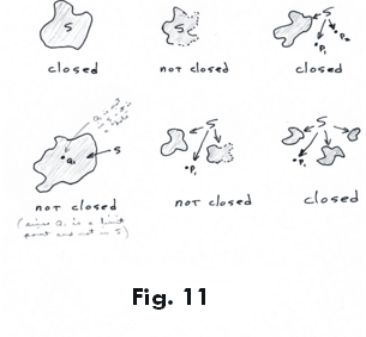
Point sets in one, two, three and n-dimensional Euclidean spaces. Neighborhoods, closed sets, open sets, limit points, isolated points. Interior, exterior and boundary points. Derived set. Closure of a set. Perfect set.
Answered: Theorem Let D be a closed and bounded… | bartleby
SOLVED: Prove that every finite subset of R^n is compact. Show that Ap Az is a compact subset of R^n if and only if A1, A2, ..., An are compact subsets of
Topology: More on Compact Spaces | Mathematics and Such
6. use the definition of a compact set to prove that the union of two compact sets
Compact space - Wikipedia
SOLVED: In the lecture, we proved that a set E ∈ ℠^n is compact if and only if it is closed and bounded. In this problem, we will explore whether this
general topology - Visual representation of difference between closed, bounded and compact sets - Mathematics Stack Exchange
Math | PDF | Compact Space | Metric Space
Let $A$ be a closed and bounded subset of $\mathbb{R}$ with the standard (order) topology. Then $A$ is a compact subset of $\mathbb{R}$. - Mathematics Stack Exchange
Analysis WebNotes: Chapter 06, Class 31
Compact Space: General topology, Metric space, Topological space, Closed set, Bounded set, Euclidean space, Bolzano?Weierstrass theorem, Function space, Maurice René Fréchet, Mathematical analysis : Miller, Frederic P., Vandome, Agnes F., McBrewster, John:
SOLVED: Set is closed (a bounded set). Which of the following sets in R' is compact? a. x,y,z: 2 < x+y+2 < 4 b. x,y,2:k+y+d<s c. x,y,z: -1 < x < y <
Compact, Open, Closed and Bounded Sets
Introduction to Real Analysis - ppt download
Examples of Open, Closed, Bounded and Unbounded Sets - YouTube
Compact Sets are Closed and Bounded - YouTube
calculus - What is the difference between "closed " and "bounded" in terms of domains? - Mathematics Stack Exchange
general topology - Determining if following sets are closed, open, or compact - Mathematics Stack Exchange
Closedness of Compact Sets in a Metric Space - Mathonline
Conpact metric spaces - GVN E
Solved Problem 5 (Fancy example of a closed and bounded set | Chegg.com
Bounded set - Wikipedia
Open Set, Closed Set, Bounded Set, Compact Set, Connected Set: Topology part-3 - YouTube
